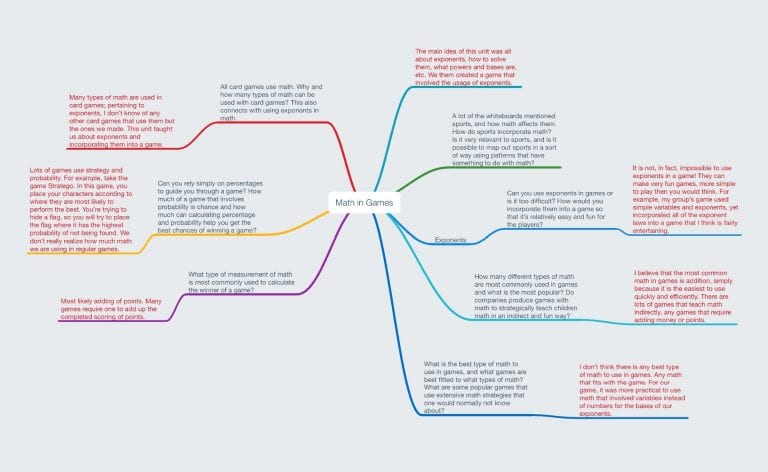
Hello friends, and welcome back to my blog. It’s about time we finished up another unit in Scimatics, and of course, with the wrapping up of a project comes a reflection, and with a reflection comes…. a blog post! This unit was all about using math in games, and more specifically, exponents. 

Before every unit, we begin with a Project Start Mind Map, where we display our expectations for the upcoming unit. As you can see, my inquiries in the Mind Map are in black font, and the answers that I came up with after completing the unit are in red. Some of these questions were general, and not very specific to exponents, simply because I didn’t know what exactly to expect in the unit. But as we progressed through it, our main focus was definitely exponents.

Exponents involve many different layers of math; squaring, cubing, variables, addition, subtraction, division and multiplication. We learned about BEDMAS (brackets, exponents, division, multiplication, addition and subtraction). We also learned about the basic exponent laws, and were able to utilize these laws in our project. To practice using exponents, we completed sheets of work with different challenging equations. Having a basis with exponents supported us to complete the large portion of this unit; a project about games in math, using exponents!

The project began with thinking of an idea for a game that was either adapted from an already established one or a completely new idea. My partner Alex and I went through a couple ideas, first considering a rendition of Pokémon with exponents, but this was too difficult to include all the exponent laws with. We then moved on to a go-fish sort of game, where you would try to complete an equation by asking your partner for the pairs of exponents from a deck of exponent cards. This, however, was too difficult and couldn’t involve any simple solving of equations. Making several drafts of this game helped refine it; we started off with a draft that was faulty, and didn’t use all of the exponent laws. Then, we decided to replace the bases of the exponents with variables; for example, instead of having 5 to the power of three, we would have A to the power of three. This made it a lot easier to manage the exponents, and we were able to include all of the exponent laws. Instead of having to add up the entire equation, it just involved adding the exponents alone, with the variables.

The first curricular competency that we used in this project was “Demonstrate and apply mental math strategies.” This is shown through the quick solving of the equations using the exponent laws. In order to finish the equations, you must know the exponent laws and where to add or subtract the exponents within these laws using mental math.

The second curricular competency we represented was “Represent mathematical ideas through concrete, pictorial, and symbolic forms.” By changing the answer cards to red, using simply variables to identify the bases of the powers in the equations, and having cards played down in general, we exemplified the math with symbols, and shortened the process of solving the equations.

The third curricular competency I feel that I learned a lot more about was “Using logic and patterns to solve puzzles and play games.” When we first began the project, I had no idea how we were going to be able to incorporate exponents into our game. By the end of the unit, we can all successfully use the exponent laws and math to play the games that we came up with.

The final curricular competency that I am choosing to include is “Connect mathematical concepts to eachother and personal interests.” This might sound a lot different than what we included in our game, but when you think about it, this competency relates to our game quite well. The particular games that we based our own off of are Go Fish and Bingo. Relating these games and adding in a mathematical element is “connecting mathematical concepts with personal interests.”


When we finished combining our ideas, I decided on a name: Pogogo! It’s because our game was based off of exPOnents, GO fish, and binGO. Pretty clever, huh? 

I printed up a good copy of our cards, and refined them a bit more after practicing. Overall this unit was super fun, because it was such a cool idea to combine exponents and games into one. 

 

 

 

 

 

Here are the instructions to our game: 

This game is similar to Go Fish.

There is a deck of 68 cards. Each card has a variable on it, with a power: for example, a common card could be A to the power of three. There are also cards that have no power and are simply a variable. There are also brackets cards with powers, and answer cards, with variables and powers. The answer cards are red. 

There are two players. Each player gets a template sheet with 3 mathematical equations on it. Each equation is composed of variables and powers. In order to play the game, you get dealt a deck of 5 cards. If any of the equations on the template have variables with powers that appear on your cards you can play them on the template and setting the used card in front of you so that you remember which cards you’ve discarded and which parts of the equations you’ve completed. For example, if I had an A to the power of three card in my deck, and one of the equations also uses A to the power of three, I would place my A to the power of three card beside my template to show that I’ve found that part of the equation. 

The objective of the game is to find every pair of variable + powers in your equation template in the deck by asking the opposing player if they have a variable and power card that matches your pairs of variables and powers. For example, if player one’s equations have a C to the power of two, player one will ask player two, “Do you have a C to the power of three?” If player two does have a C to the power of three in their deck, they will give it to player one, and player one can cross off C to the power of three on their equation template and discard the card. 

The equations on the template also require an answer, which is on a card in the deck somewhere. The answer cards are red. The equations are simple, so solving them will tell you what card you need to look for when playing the game. If you’ve crossed off all of the variable + power pairs in one equation, all you need in the answer card to complete that certain equation. The first person to complete all three equations on the equation templates wins. 

The brackets cards are for equations that have brackets. In order to complete this equation you need to play a brackets card. The brackets cards will have powers, and so will the brackets in the equations. You must play a brackets card that has a matching power to the brackets in your equation. 

In order to win the game, you must find the cards for all of the parts of your equation. If your equation has brackets and two variables + their powers, you have to acquire the two variable + power cards matching to the equation, a brackets card with a matching power, and the answer to the equation.

This unit has been a pretty interesting one! I hope that in the future we will have the chance to do more units like this one.