Posted by

theryns

Posted on

October 13, 2021

Posted under

Summative post, work

Comments

Leave a Comment

Epidemic Exponents!

Hello, and welcome. I am back to school, and starting this year in scimatics with exponents! In the first scimatics project this year, Game of Exponent Laws, I learned how to evaluate exponents, exponent laws, and more. So without further ado, here is the post.

To kick of the project, we did a quick activity were we made up games that used one and two dice. We got into groups of four, and started working. And here are the rules we came up with:

Rollie poll-E

Assemble all the players in a circle. Decide who will roll first, and have them roll the die. If their roll is a 4, 5, or 6, add the roll to their point tally. If their roll is a 1, or 3, subtract their roll from their point tally. Point tallies cannot drop below zero, and if they reach twenty, that person wins. If they roll a 2, they get to roll again and multiply that roll by two and add it to their point tally.

Rollie poll-E 2.0

To win, gain 5 points. You gain a point when you correctly answer a question faster than your opponent(s). Choose someone to roll each round, and have them roll the two dice. Once the dice have settled, every player starts solving the math problem. If the dice are both even, devide the greater roll by the smaller one. If the dice are both odd, multiply them. If the dice are odd and even, add them together. Once you figure out the answer, say it aloud, and if you are the first to solve the problem, you get a point. Decimal points are allowed for answers. If the roll has a 1 then subtract 1 from the other roll

(Special thanks to Jocelyn for thinking of the names)

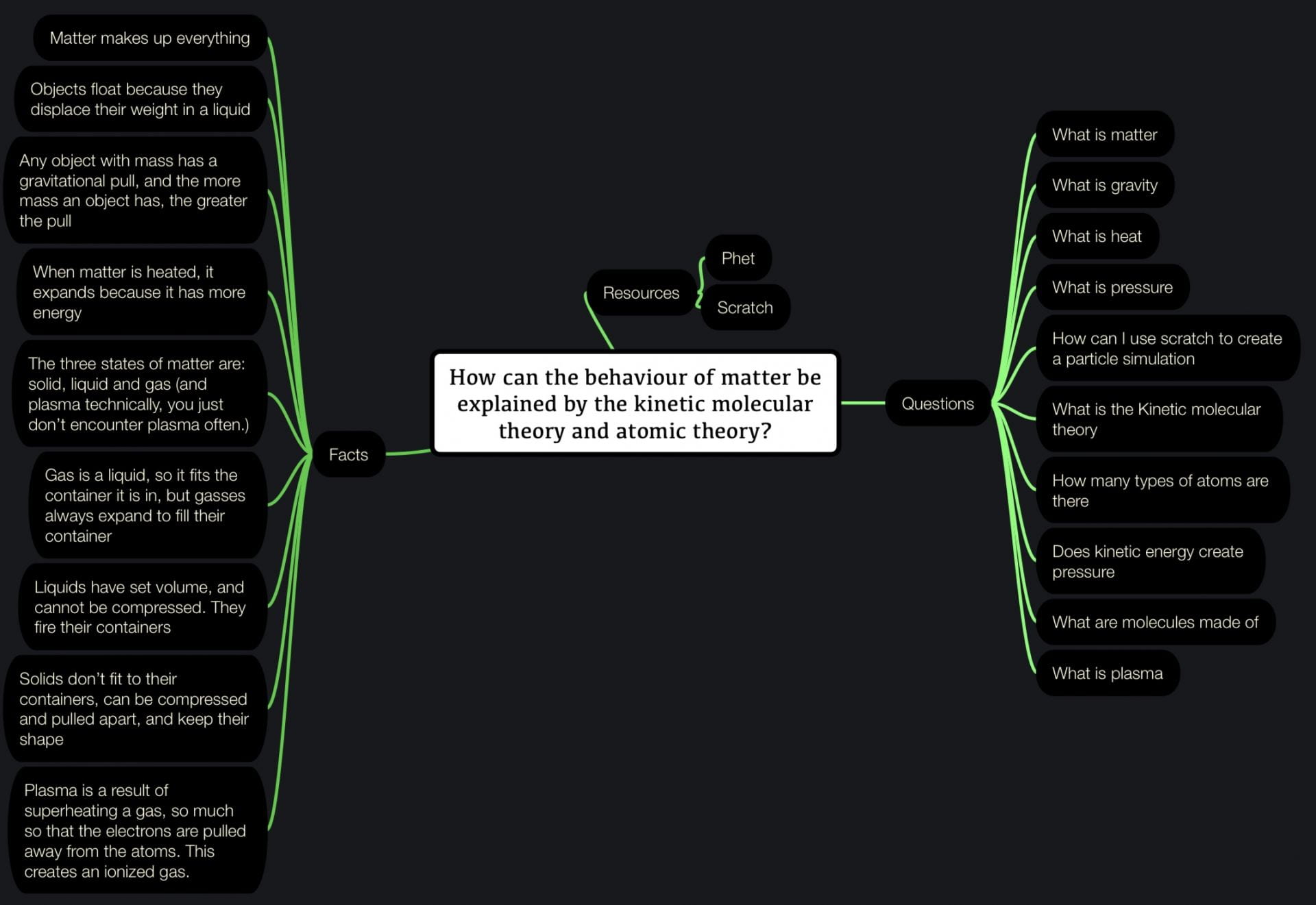
So, as common with scimatics projects, we all were supposed to make a mind map that’s outlines what we already know and what questions we have.

Now, in this project, the milestones were not a linear process, but in a slightly erratic way, with the milestones not coming in numerical order. So, for the sake of this post, I will tell you about the events of this project in chronological order.

After these first assignments, me and my partner started brainstorming Ideas for our game. Our first milestone was milestone four (confusing). For this project, everybody was given a partner, and together you and your partner would make a game that uses exponents as a central mechanic. So, eventually, me and Aliciah decided to make a game about viruses. Our idea was quite similar to pandemic: contagion, which is a game were each player is a virus trying to exterminate humanity. Our first draft of our rules are here.

Throughout the next week, we updated our game rules and did some exponent practice, and eventually landed on this set of rules:

Epidemic Exponents Final Rules.

After making these final game rules, it was time to make our game board and pieces.

And, of course, there were curricular competencies for this project, which are listed below.

Applying and innovating: Contribute to care for self, others, community, and world through personal or collaborative approaches.

All class time is used efficiently for learning without distractions. All group members contribute equally.

I used my class time well, and I think that is reflected in the quality of my work. My partner and I shared equal part in the workload for this project.

Reasoning and Analyzing: Use logic and patterns to solve puzzles and play games

A clear and simple points system and win conditions for the game are carefully designed.

Points system is clearly represented by physical game pieces, and finding out who wins a game is easy and concise.

Communicating and Representing: Represent mathematical ideas in concrete, pictorial, and symbolic forms

A set of clear, complete, interesting and personalized instructions are created for how each player takes their turn. Examples are included. The game design uses at least 4 different exponent laws and using these laws is integrated into each player’s turn.

Our game features game rules completely written from scratch, with our own ideas and examples of gameplay and game pieces. There are over four exponent laws included in our rules.

And that concludes my blog post for today! Thanks for reading this far, and if you want to check out my partner Alicah’s blog, click here.

See you in the next post, bye.

Posted by

theryns

Posted on

June 20, 2021

Posted under

Summative post, work

Comments

Leave a Comment

Don’t Eat Rat Feces!

Today, I am writing a summative post about my latest, and last project of the year. This project is called Comic Cells. I learned a ton from this project, from what subsequent endocytosis is to why you shouldn’t eat rat poo. So, without further ado, here is the post.

As with all scimatics projects, we started off the project with a mind map of existing knowledge, question, sources, and anything else about the topic. Here is mine:

For the second milestone of the project, I created a wanted poster for a disease containing the date of discovery, how it affects cells, it’s mortality rate, and more.

Then I started working on a storyboard to guide the making of my comic. The storyboard was a very rough guide to the comic, and some parts were not even in the final comic.

Then I started to research a TON of facts about the virus I chose. (Hantavirus) To read more about hantavirus, veiw the sources down below. I learned a ton about cellular processes, and then started drawing pictures for my comic. I am not the best at drawing, so this was a hard task for me. However, I a very proud of the final comic, which is the namesake for this post.

Don’t Eat Rat Feces

And, as with all projects, there were core competencies I worked towards throughout the project. They are:

1. Questioning and predicting: Demonstrate a sustained curiosity about a scientific topic or problem of personal interest.

All class time is used for learning and creating a comic book story about cellular processes and/or diseases. I think I used almost all of my class time efficiently, but even so I still think I could’ve worked slightly faster in class and had less homework after school. But it worked out in the end, which is good.

2. Scientific communication: communicate ideas, findings, and solutions to problems using scientific language, representations, and digital technologies

Correct vocabulary and accurate diagrams are used. At least 10 interesting science vocabulary words are included in the story. I used more than ten science words in my Story, and I think my diagrams are concise and accurate at what they represent.

Evaluating: Demonstrate an understanding and appreciation of evidence

Cell/bacteria/virus characters interact in a scientific way. Symptoms and logical outcomes of the chosen disease/cellular/ body process are integrated into the story. In my story, the reaction to the virus is realistic to real-life cases, and the outcomes are on the probable side.

Sources:

Thanks for making it this far. If you liked this post, make sure to check my other ones here. See you in the next post! Bye.

Posted by

theryns

Posted on

May 11, 2021

Posted under

Summative post

Comments

1 Comment

Atoms

As you can probably tell from the title, this project was one about atoms (and molecules, Kenetic energy, etc…). We spent about three weeks learning, coding and thinking to answer the driving question for this project: how can the behaviour of matter be explained by the Kinetic Molecular theory and the Atomic theory? So, without further ado, here is the post.

We started this project with a mind map and an experiment/magic trick. We wrote the mind map about what we already knew about matter, and then all of our questions about it.

For the demonstration of atomic and molecular theory, the teacher performed a trick using a sealed bottle filled with water and an eyedropper.

The trick works by utilizing pressure. When the bottle is not squeezed, it looks like this:

But when the bottle is squeezed, the pressure increases, forcing the eyedropper down, and if you are subtle, it looks as if you magically made the eyedropper go down.

Squeezed bottle with the eyedropper down

One really cool activity was called the gemstone identification challenge. The whole class partnered up to measure the volume, weight, and then calculate the density of a few stones. The class average density was 3.74 grams per millemeter, and the closest density to that was that of colourless topaz, so we confirmed that the stones were colourless topaz.

For milestone 2, we created accurate models for our coded project. In order to make our simulations or games follow this competency: Several different atoms/molecules, different states of matter, and particle motion are represented in the finished product. A historical model of the atom is chosen and implemented, we created some sort of model and text.

In order to create realistic and functioning models of atoms, molecules, and in my case quarks, I worked on three slides of information and graphics. It took three other versions to create to the one shown below.

The final three slides (to veiw them in higher detail, click here)

The next week was mostly spent learning more about matter and coding or refining our scratch projects. Then we did milestone four, which was a coding plan for the rest of the project. This was my milestone four coding plan:

Features:
Press space to show Bohr models
Press M to mute music
Press N to unmute music
Press Q to create more clones
Press 1-3 to change molecule type
Gravity that can be turned on and off
Click the reset button to reset the simulation
Use the temperature slider to change how fast the particles move.
Setting the temperature to zero will stop the particles from moving, other than gravity acting on them.
You can create different states of matter by adjusting the temperature and gravity.
you can adjust how much gravity there is.
You can move between subatomic particle models, Bohr models, and no models by pressing space bar twice This kinetic molecular theory is included in the simulation when the particles move. They follow the Kinetic molecular theory.

After creating a plan, I continued coding my scratch project until it was completely done and polished. If you want to check out my simulator, click here. After all was said and done, I created a summative mind map of the project, which helped round of the end of the project.

As with all projects, there were curricular competencies which you can see below:

Questioning and Predicting: Demonstrate a sustained curiosity about a scientific topic or problem of personal interest.

All class time is used efficiently for learning without distractions. I used all my class time efficiently, and I am very proud of my final product.

Scientific Communication: communicate ideas, findings, and solutions to problems using scientific language, representations, and digital technologies.

Several different atoms/ molecules, different states of matter, and particle motion are represented in the finished product. A historical model of the atom is chosen and implemented. I have three different molecule designs: H2O (water), carbon dioxide (CO2), and ozone (O3). I also have three Bohr models of the elements: carbon, hydrogen, and oxygen, And finally two subatomic models of protons and neutrons.

Reasoning and Analyzing: Use logic and patterns (including coding) to solve puzzles and play games.

An interactive Scratch coded matter simulator or game is created with logical conditions and functional user controls. I created a simulator with four variables that the player/user can change, and extra aesthetic changes as well. The user can change limits all the variables, and the layout is logical and easy to use.

Thanks for reading my post! I had a great time doing this project, and i am sure to do more, so stay tuned .Even though I have featured it already, just in case, here is the link to my scratch matter simulator. Thanks to my friend Noah for all the coding help and feedback. If you want to check out his blog, click here. See you in the next post!

Posted by

theryns

Posted on

January 26, 2021

Posted under

Summative post

Comments

Leave a Comment

Laser laws final post

Hello, and welcome to anotherblog post. In this post I am going to show all I have learned throughout the laser laws project. First, I’ll start with the driving question: how can I test Pythagorean theorem and the law of reflection. There are many ways to test this, but first we had to build our knowledge on the subject by completing worksheets and doing cool science experiments. For example, at the start of the project we played laser tag, were there are two teams and they both try to shoot the other team’s target with their laser, while protecting their own. There was not to much to be learned from this activity, but it was a fun intro to the law of reflection. After that we did a project start mind map:

And along the way, I added to the question section, and also answered them all in another mind map at the end of the project:

While mind maps are all fun and good, though, we still haven’t actually tested the law of reflection or Pythagorean theorem. We did a small workbook to get up to speed, and then did a really cool experiment about the wave model of light. Here is the experiment:

in the waves lab, I learned a lot about the nature of light, and how there are multiple models that can be used to define it. We were then split into groups, then did an experiment on Pythagorean theorem. In My groups’s experiment, we tested to see if you can use Pythagorean theorem to get the values of the two legs with only the hypotenuse. The answer was no, but if you know that the legs are the same you can do it.

In my second milestone, we did a khan academy test to check our understanding. Our third milestone was yet another experiment, this time testing if the law of reflection can be used to make shapes.

Law of reflection experiment Click here for full experiment

After this, we started on milestone four, the design for our laser triangle. This design may or may not be used as the final design, but it is a crucial step nonetheless. There were three revisions of this, but here is the final one:

Then, it was time for the final design. The groups started to set up the mirrors, prepare the laser circuits, and do all-around finishing touches.

Then all the groups set up their projects near the smoke machine, then we all got really cool views of our work coming together.

I overall learned a ton from this project, from how to measure est sides of a triangle to the different models of light

And, finally, the curricular competencies:

The first of three, questioning and predicting, is about ‘‘Demonstrating a sustained intellectual curiosity about a scientific topic or problem of personal interest’’ I think that I did this quite well, as I was on task and very interested in the class.

In the second, Questioning and predicting, you must ‘‘Demonstrate a sustained intellectual curiosity about a scientific topic or problem of personal interest’’, and I did well in this, because i had so many questions about the law of reflection and Pythagorean theorem. Luckily, google search, textbooks, and class resources exist.

The last but not least competency is applying and innovating: cooperatively design projects. I believe I did this well because our group got along well and our final product checked all boxes

And, the answer to the driving question: out of the many ways you could test the law of reflection, by far the simplest is to just grab a mirror and shine a laser on it in a dark room, and take a picture and measure the angles in it. To test the Pythagorean theorem, you could draw right triangles with random side lengths, then use Pythagorean theorem to solve for the missing edge. Then, check your answer using a ruler or, the measure app.

Posted by

theryns

Posted on

December 18, 2020

Posted under

Summative post

Comments

Leave a Comment

Tectonic Chances Summative post

Hello, and welcome to anotherblog post! In this project, the driving question was: how are thematic and mathematical elements used in board games?

The answer to this is: they can add a touch of realism, role playing, or just a cool element to your game. Thematic and mathematical elements can and are used in board games all the time, for example: chess; which uses medieval figures to add a slight bit of logic and realism to the game, which helps connect players to the game a bit more. In other versions of chess, they use other themes to make the game more applicable to different audiences. Or in games like pandemic: contagion, where tons of different chances are balanced to create a fun and diverse game.

Anyway, to get this answer, we had to do many activities, like learning about tectonic plates in order to make a game about them, doing a mind map, listing the scientific elements they will be in our game, and finally making actual game rules and a playable game and presenting them to other groups in the best way: playing them!

The first thing we did was make some rough game rules (which, in my group, weren’t used later on) on whiteboards.

Here is the first iteration of our game rules

This was the original mind map, but my game was changed a lot later

And, as with each project, there were curricular competencies that everyone strived for.

The first: evaluating; demonstrate an understanding and appreciation of evidence. in the criteria for this competency, it states that there should be evidence of 10 key science concepts in your game, and game pieces should visually represent tectonic concepts. I think I this because my game had 10 science concepts: convection currents, mid-ocean ridges, volcanoes, earthquakes, ridge push, subduction, reverse faults, normal faults, and strike-slip faults. Speaking of which, click here for said game rules.

Onto the second competency, questioning and predicting. I think I used most of my class time efficiently and well, because I finished all work on time and did most of it in class. I also handed in first drafts of my work early for feedback.

The third competency, understanding and solving, is all about demonstrating understanding of mathematical concepts through play, inquiry, and problem solving. I think I did this because my game has lots of probability that is calculated at the end of the rules. At the end of my rules, there are multiple probabilities calculated correctly, and there are examples of turn outcomes stated.

Posted by

theryns

Posted on

December 17, 2020

Posted under

work

Comments

Leave a Comment

Tectonic game rules

Tectonica Rules

Object of the game

The object of the game is to either push your tectonic plate far enough to win, or push the opponents plate back enough for them to lose.

How to setup:

To set up the board all you have to do is place the tectonic plates four spaces in from the edge of the board.

Numbers of players:

This is a two player game.

What a common turn looks like

In most turns, you will:

1. Roll die

2. Hold which die you want to keep and re-roll the rest

3. Repeat step 2 once more

4. Move tectonic plates

5. Roll for earthquake (if you want and do not have the volcano chip)

In-depth description of each step:

Step one: Roll die

In this part of your turn, you roll all the die, and pick which ones you want to keep.

Step two: Hold die

In this part, re-roll the die that you do not want to keep.

Step three: Repeat step two

Just repeat step two.

Step four: Resolve dice

Once you have rolled the die, you must resolve what they do.

How to resolve dice:

If you rolled more than one of a 1, 2, or 3, move your plate forward on space for each die in the streak. This is the start of making a convergent plate boundary.

If you get a ascending streak, you move the opponents plate back one space for each die. You must have at least three die in the streak though. This is how a mid-ocean ridge is formed.

For each six you roll you get to move your plate one space forward. This is another way to create subduction.

If you roll a five or four, you can choose to try to make a volcano. To make a volcano, you must choose any number from one to six, and roll the four or five you are using in the creation of the volcano. These die also cannot be used in other streaks. If you roll the chosen number, you successfully make a convergent plate boundary, which also leads to a volcano. If you make a volcano, you get the “volcano” chip, which allows you to have one extra re-roll each turn. The most recent person to make a volcano should always have the volcano chip. You can try to make a volcano more than once in a turn.

Other rules:

1. If both of the plates are within four spaces of the middle, they form a convergent plate boundary. This makes it so you cannot move your player forward, only move the other player’s plate back. This is because of convection currents pushing the plates apart.

2. If you move the other player’s plate back past the last line, they lose. If a player’s plate crosses or lands on the middle line they win, because they have made a convergent plate boundary.

3. If you don’t have the volcano card, you can also try to cause an earthquake. To cause an earthquake, you must choose any number from one to twelve except seven, and then roll two die. If the sum of the two die is the same as the number you choose, you create a reverse fault, so the enemy player cannot move their plate for two turns. If you roll and it is within one of the number you choose, you creat a strike-slip fault, and the enemy player cannot move their plate for one turn. If you roll a two, you create a normal fault, and this causes your plate to move back two spaces, and on your opponent’s next turn, if they have a roll that is supposed to move their plate forward, they actually move it back that number of spaces.

4. If the first two turns have rolls that win the game, re roll them immediately.

Probability:

The chance of rolling a ascending streak of six on your first roll is ¹⁄₄₆₆₅₆, but for every time you re-roll your chances increase. This is because if you roll six die, and there is a one in 6 chance of rolling the right number on each, the equation is ⅙ x ⅙ x ⅙ x ⅙ x ⅙ x ⅙ = 1/46656.

The chance of getting three threes on your first roll is 1/216, but re-rolling gives a much higher chance of getting it. This is because of if you roll a three on one of the die the chance of rolling another two three’s is less likely. The equation of rolling this is 1/6 x 1/6 x 1/6 = 1/216.

A Cool Site

My PLP School Blog.

Tag Archives: science

Epidemic Exponents!

Don’t Eat Rat Feces!

Atoms

Laser laws final post

Tectonic Chances Summative post

Tectonic game rules